A Review of Finite Element Modeling for Anterior Cervical Discectomy and Fusion
Article information
Abstract
The cervical spine poses many complex challenges that require complex solutions. Anterior cervical discectomy and fusion (ACDF) has been one such technique often employed to address such issues. In order to address the problems with ACDF and assess the modifications that have been made to the technique over time, finite element analyses (FEA) have proven to be an effective tool. The variations of cervical spine FEA models that have been produced over the past couple of decades, particularly more recent representations of more complex geometries, have not yet been identified and characterized in any literature. Our objective was to present material property models and cervical spine models for various simulation purposes. The outlining and refinement of the FEA process will yield more reliable outcomes and provide a stable basis for the modeling protocols of the cervical spine.
Introduction
The cervical spine is one of the smallest and most intricate joints in the human body [1]. Cervical disc herniations are a problem caused by repetitive cervical spine loading [2]. The severity of loading needed also decreases as the age of involved patients increases [3]. This is due to a lack of nutrient supply to the intervertebral disc; resulting in natural wear and decreased performance with age, a phenomenon known as cervical spondylosis [4]. If the disc degenerates, the cervical spine’s stability will be compromised, and the intravertebral disc height will change [5]. The decrease in foraminal spacing can result in cervical radiculopathy and the compression of nerves causes great discomfort and reduced quality of life for the affected individual [6].
The first attempts made at addressing this were through the fusion of the adjacent vertebra in a technique known as anterior cervical discectomy and fusion (ACDF) established in the 1950s [7]. The intervertebral disc and osteophytes are removed during this treatment, and the area of the spine is decompressed. Then, to maintain foraminal spacing and to encourage a stable site for osseointegration, an adequately sized cage and bone graft are implanted [8]. Shortly after, plate instrumentation was introduced to help regulate the stresses of the cervical spine. A variety of surgical techniques and hardware have been developed in addition to the standard anterior plating, to improve the biomechanical postoperative state. Some adjunct structures that have been applied include lateral mass and pedicle screw systems, facet replacement devices, and cervical disc replacements for multilevel procedures [9]. For the treatment of cervical disc problems, the golden standard has not yet been discovered [10]. To better meet the needs of the system, more information on the generalities and mechanics of the cervical spine is required. Many techniques have been used to learn more about the cervical spine [11].
The finite element is important for predicting spine mechanics in situations where in vivo and in vitro models prove insufficient. In the determination of internal loads, stresses, and strains in spinal tissue, numerical models have been used [12]. Simulation results from numerical spine models can be employed to gain insight into the inner workings of the cervical spine [13]. Moreover, virtual models can display information previously unobtainable via physical models, such as stress distribution in the intervertebral disc. Gradually, more accurate cervical spine modeling has increased the accuracy of the guidance of spine surgery and the new design of cages. The only notable drawback is that greater computing power is needed. This is controlled by converting models into somewhat less computationally intensive versions. The findings they offer will still be quite accurate if they pass convergence tests and are validated against data that is known to be accurate. Cervical spine modeling has been the subject of multiple reviews of the literature, but there have not been any that contrast cervical spine models with material models. The limitations of the material models and cervical models were not compared and discussed. We will therefore focus on reviewing the material property models and cervical models for potential interest to the surgeons and biomechanical engineers.
Material Models
The behavior of a given material under loading is described by material models. Based on how accurately they depict the kind of material being described, material models are chosen. Different material models may be applicable for the same material since they can yield results that are more consistent in some movements while visibly less accurate in others. However, a standard for which models are most applicable for each anatomical structure has emerged from the use of these models in a wide variety of loading conditions.
1. Vertebrae
The cervical vertebra could be represented by up to three different structural elements. The exterior cortical bone and the interior cancellous, or trabecular, bone can be used to simulate the vertebral body [14]. Some research place greater emphasis on the transverse process, lamina, and spinous process as more central to the results of the study; in that literature, a third body is added for the posterior region to have greater accuracy in the model. The cortical bone and cancellous bone are described in some sources as orthotropic, however, the vertebra is typically approximated with an isotropic elastic model. The posterior body is typically modeled in the same way as the cancellous bone when it is included [15]. The posterior bone is quite consistent across the literature with the exception of Kopperdahl et al. [16] who employed an isotropic, power-law plasticity material model for the diagnosis of bone damage [15,17–19].
2. Endplate and facet joints
The vertebral, or bony, endplate and the cartilaginous endplate make up the endplate structure. Typically, an isotropic elastic model is applied to the facet joints [20]. To ensure a smooth passage of forces between the facet joints, Kumaresan et al. [21] devised a simplified facet joint model similar to the fluid-based facet joint model.
3. Intervertebral disc
The nucleus pulposus and the annulus fibrosus (AF) are the two parts of the intervertebral disc. Since the nucleus pulposus is a viscoelastic material, the loading condition affects how it behaves. In addition to the traditional isotropic elastic model, an occasional hyperelastic model may be utilized; some literature even regards the nucleus as a fluid of varying compressibility [22,23]. A single section was successfully modeled in quasi-static conditions by Yang and Kish [24] using a fluid material model with a bulk modulus of 1.720 GPa. However, the nucleus pulposus was modeled using the linear viscoelastic model to recreate the whole cervical spine model [25].
The AF is considered as two parts in literature, a ground substance and several layers of angled fibers. Hill [26] modeled AF ground substance with an isotropic, nonlinear strain-energy function while still preserving the compressibility of quasi-static simulations such as that presented by Storakers [27]. The annulus ground has been represented utilizing an isotropic elastic model, hyperelastic models like the neo-Hookean, the Mooney-Rivlin model, or as a Hill foam [15,17,28].
The annulus was modeled by Cassidy et al. [29] using five layers whose angles changed depending on the radial position. According to Eberlein et al. [30], a nonlinear tension-only fiber model was merged with a novel Hooke hyperelastic base material to create an anisotropic constitutive model.
4. Ligaments
Numerous ligaments with various stress-strain relationships reside in the cervical spine, although their general behavior is constant. As a result, in each analysis, the ligaments in the area are all modeled using the same material model. According to the stress-strain relationship or the force-displacement curve, the ligaments are classified as either a hyperelastic material or a tension-only element [15,17,18,28]. These elements are generally tension only and occasionally include a cross-sectional area [19]. In their investigation of the high rates of ligament deformation, Yoganandan et al. [31] found that viscoelastic effects were more prominent in complete spine models, necessitating the use of a dynamic scaling factor.
5. Muscles
The Hill-type muscle’s passive muscle is the only part that adheres to a conventional material model. A bilinear elastic model with non-linear dampers and a hyperelastic Ogden model with linear viscoelasticity are the two fundamental models for the depiction of the passive muscle. Within the usage of either of these models, no difference exists in material parameters between muscle groups.
6. Spine hardware
Isotropic elastic materials are commonly used to describe surgical devices. Because the standard materials utilized in this method (titanium, cobalt chrome, stainless steel, PEEK) all adhere to the same material model, there is very little variation.
Material Properties
There is great variation in the material properties utilized in FEA for ACDF. The variety in the cadaver specimens used for the development and validation of the original models is the cause of many of these variations. Tables 1–3 list all pertinent material parameters [15,17–20,23,28,32–34].

Details the material model and properties of the main anatomical structures in the cervical spine, as presented in the literature

Details the material model and properties of the cervical spine ligaments as presented in the literature
1. Vertebrae
The vertebra is segmented into 2 or 3 components so that each one can be given particular attributes and a more precise model can be produced. Since the cancellous bone has a softer interior than the cortical bone, the cortical bone is represented with a greater modulus. The characteristics employed for the cortical bone and cancellous bone appear to differ significantly. Additionally, a different set of material qualities are used in the posterior body [35].
2. Endplate and facet joints
The bony endplate is the only portion represented in FEA, despite this not being defined in the literature. The endplate employed in FEA has material characteristics that are identical to those of the bony endplate. The justification is that the cartilaginous endplate was sufficiently similar to the intervertebral disc properties at intact disc sites and fusion sites, and the surgical procedure typically requires the removal of this softer part of the endplate. The element type and contact settings typically define the facet joints.
3. Intervertebral disc
The modulus and Poisson’s ratio of the AF ground does not vary. None of the material models employed have much diversity in the parameters for the AF ground. The AF fibers typically sit at a modulus around 400–500 MPa and a Poisson’s ratio of 0.3, but some extremities exist with a much lower modulus. There is some variety in the nucleus, with the majority opting for a modulus of 1 or 3.4 MPa. Natarajan et al. [18] reports using 3.0 MPa. Other models’ characteristics, like those of the hyperelastic models, vary slightly.
4. Ligaments
The ligaments material properties are what distinguish the cervical spine’s ligaments from one another. This is because their main description is their stress-strain curves. According to the results of Yoganandan et al. [36], the ligament’s force-deflection response can be divided into three separate zones.
5. Muscles
The same general properties and varying geometric parameters are used to represent each component of passive muscle. Since the physiological cross-sectional area is used in the calculation of force output, geometric conditions are important to the material characteristics of the active muscles.
Most literature on the cervical muscles references active muscle contraction. In most FEA, the forces generated by the muscles are depicted as a straightforward moment. The construction of these whole spine models was based on investigations by Winters et al. [37–39] and involved the separation of force parts of muscle usage into independent forces, the acting location, direction, and amplitude of which were estimated using numerical models. According to Winters and Stark [37], neuronal excitation and active state dynamics make up muscle activation in the Hill muscle model. The active muscles are represented by a nonlinear force: stress relationship based on the maximum stress that can be withstood by human muscle.
6. Spine hardware
Most instrumentation is modeled with material properties for titanium [40,41]. By lowering the material characteristics of the plate, cage, and screw structures, several spine hardware models have attempted to assess unique instrumentation [41,42]. Huang et al. [43] concluded that gradient porosity has proven effective in reducing the subsidence and stress concentrations surrounding the cage. The three-dimensional cervical spine model created by Choi et al. [44] used biodegradable plates and screws, and the results showed significant rates of graft extrusion and subsidence.
Finite Element Method
The degree to which a mathematical solution accurately represents an actual situation depends heavily on the finite element method. It is considered that, aside from the facet joints, all anatomical features in a healthy cervical spine are bonded. Mesh convergence testing must be used to verify the element size. Researchers choose an element type based on the most realistic representation of the structure’s natural behavior, and the model is finally deemed acceptable through validation with experimental data and existing literature.
1. Vertebrae
Hexahedral, tetrahedral, or shell elements are used to simulate the cortical bone [45]. The standard modeling of cancellous bone and posterior bone employs hexahedral elements for the cancellous bone and tetrahedral elements for the posterior [15], though some models have opted for isoparametric elements [18].
2. Endplate and facet joints
Tetrahedral or shell elements were used to model endplates [32]. The facet joints are synovial joints that link two vertebrae during the articular process. To imitate the behavior of a synovial joint, these joints are modeled as solid element cartilage bodies with assigned contact elements [46]. Although gap contact elements have been used, sliding contact elements are the norm in the literature.
3. Intervertebral disc
Hexahedral elements are used to simulate the AF ground [47]. The AF fibers are modeled as solid or tension-only elements [15]. Solid or fluid elements have been used to represent the nucleus pulposus [18].
4. Ligaments
The cervical spine is covered in a long array of ligaments. ACDF mostly occurs in the mid and lower cervical spine; ligaments of the occiput, atlas, and axis are excluded. The ligaments left remaining are the anterior longitudinal ligament, the posterior longitudinal ligament, the interspinous ligament, the supraspinous ligament, the capsular ligament, and the ligament flavum. Each of these ligaments is modeled as spring, truss, or spar elements.
5. Muscles
The most advanced variant of this typical Hill-type model includes three components: a contractile element, a passive elastic element, and a viscous damping element [48]. Active-passive muscle behavior is frequently created using the Hill-type muscle model.
6. Spine hardware
When it comes to analyzing ACDF and researching surgical hardware, the finite element method is crucial. The contacts of the hardware with the cancellous bone have often a frictional contact of 0.95 or bonded as a representation of the postoperative condition. The contact with the endplate is typically set as a frictional contact of 0.5. The results of micromotion and subsidence caused by the hardware’s interaction with the cervical spine provide an indicator of the likelihood of screw pullout, cervical misalignment, and long-term issues with fusion.
Numerous cervical spine segmental models have been developed and applied for the actual events of ACDF considering the subsidence and migration of the cages, screws, and plates (Fig. 1). By comparing micromotion and subsidence, Lin et al. [49] have created a new cervical spine finite element model to analyze the effect of cage screws on the biomechanical characteristics of the human spine, implanted cage, and associated hardware. According to the findings, the cage-screw and anterior plating combination have promising potential to decrease the risk of micromotion and subsidence of implanted cages in two or more level ACDFs.

The micromotion field (A) and subsidence field (B) between the C45 bottom endplate and cage under the flexion situation.
Additionally, the effect of biomechanical strength and increased contact area was examined on the maximum von Mises stress, migration, and subsidence between the cancellous bone, endplate, and implanted cage [50]. The newly constructed models revealed that a 1 mm embedding depth appeared to be the best balance of mechanical strength and contact area, resulting in the most favorable stability (Fig. 2). The friction between the cage and the endplate was considered to be constant, which is one of the studies’ shortcomings. Moussa et al. [42] considered variable porosity cages in the spine model and they demonstrated the advantage of lowering stress (up to 14%) and strain (up to 21.7%) under severe loading combinations. Additionally, Park et al. [51] observed that using more screws reduced the probability of sinking, though not significantly. Although not significantly, increasing the screw angle decreased the probability of sinking in the allograft spacer and the screws [52]. Different fixation methods improved stability in some areas of the fusion site but worsened stability in others. Screw loosening generally increased as the plate length increased [52]. Micromotion and subsidence are lessened by rotational dynamic plating, yet too much tolerance for rotational freedom in the screws eventually becomes detrimental [53]. Segmental plating decreased the chance of screw pullout post-surgery [54].
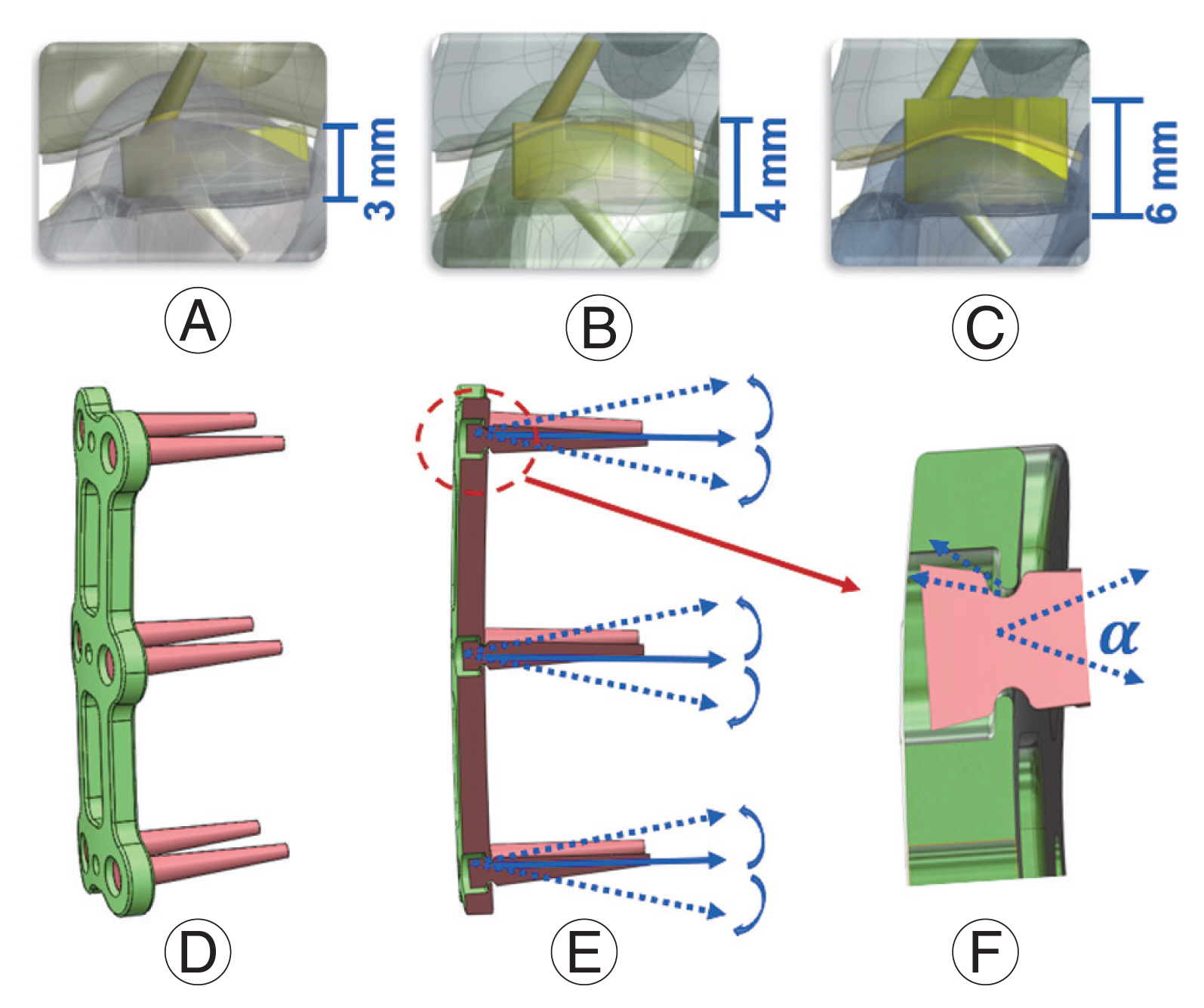
(A) C4C6 segment three-dimensional (3D) finite element (FE) with the implanted cage; (B) C4C6 segment 3D FE with the cage embedded 1 mm; (C) C4C6 segment 3D FE with the cage embedded 3 mm into the endplate/vertebra. (D) Schematic of dynamic plate model with range of motion of screws; (E) section view of the dynamic plate; and (F) geometry differences for the 18°, 28°, and 38° (α) dynamic plate.
Specificity and Inclusivity in Models
Investigators must exercise judgment when evaluating the accuracy of models. Modeling more than is necessary is ineffective and can obscure the crucial information required to comprehend a particular circumstance. Models that are overly simplified or reduced in detail can produce false results or simply leave out important elements that would provide more information about the biomechanical state of the cervical spine.
The majority of the FEA models currently utilized in literature are stitched together from patients’ CT data in mimics and meshed in a structural analysis preprocessor such as software ANSA or Hypermesh [55] (Fig. 3). As a result, the results of the FEA reflect the variation in the patient’s cervical geometry. This does not create any noticeable alteration in results. Examples of both fairly simplified parametric models and more complicated models with the muscle represented as solid parts are provided. Validated models, though varying in execution, do yield accurate outcomes. Execution differences, however, provide a wide range of outcomes that help resolve various cervical spine disorders.
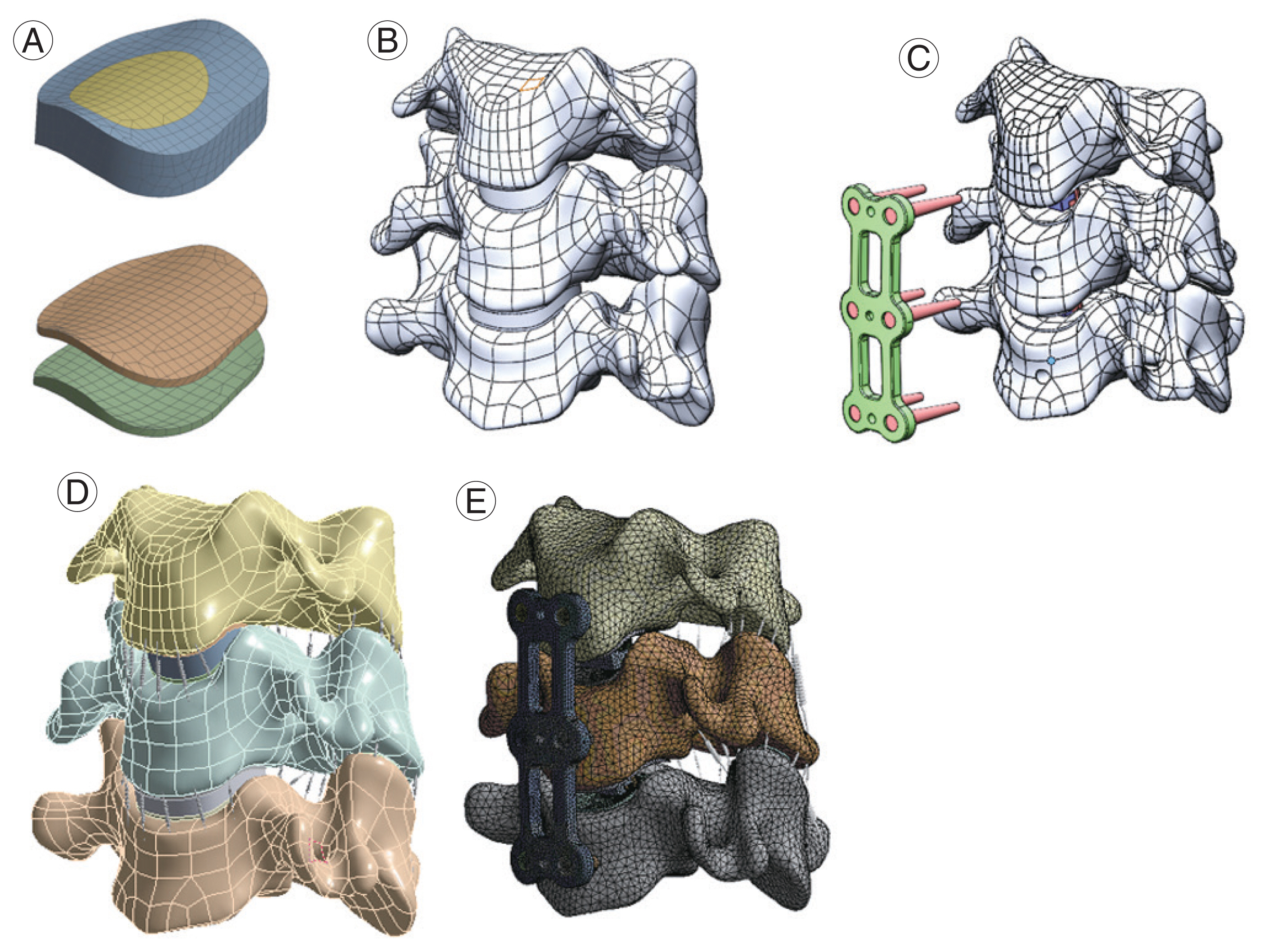
(A) Mesh of the disc and endplate; (B) C3–C5 segment three-dimensional finite element model with original disc and endplate; (C) the endplate was partially removed after implant cage; (D) C5 bottom edge was fixed and the moment was applied in the top surface of C3; (E) anterior longitudinal ligament, posterior longitudinal ligament, and disc were removed while the plate and cage screws were implanted.
1. Segmented spine models
The elimination of simulated junctions has proven to be one of the most significant reductions possible in ACDF models. When appropriate, modeling a collection of segments rather than the entire cervical spine has been the norm.
Typically, vertebra-disc-vertebra models of spinal segments are often compared to experimental data demonstrating the effects of simple quasi-static pressure on the biomechanical behavior of local tissues. To explore intervertebral disc stress distribution and pressure under compressive load, Belytschko et al. [56] created the first simplified axisymmetric model of a human spine. All models were linearly elastic, with the exception of the fiber loops, which were linearly orthotropic.
The first important cervical segmental model was created by Yoganandan et al. [13] using the geometry of the C4–C6 sections from CT scans. The material properties employed in the model were based on the model’s calibration to experimental data and the material models of the AF and nucleus pulposus were both considered as isotropic linear elastic materials. In comparison to the experimental data, the model performed well. Three years later, Kumaresan et al. [57] improved this model by including a more accurate model of the AF and a detailed model of the synovial facet joint. Intervertebral discs utilizing this new anisotropic AF model displayed a significant improvement over the experimental data compared to those constructed with linear composite AF.
2. Full cervical spine models
Compared to their counterparts, full cervical spine models are very uncommon in the literature. These are typically carried out to achieve results that would otherwise be impossible to achieve or to include extra, typically unaccounted-for systems like the muscles. The full cervical spine model usually focused on the global motion of the head rather than local tissue, unlike spinal segment models. In order to imitate the behavior of a real being, Williams and Belytschko [58] designed the cervical spine model with six degrees of freedom springs for shock loading conditions. It was successful at simulating the movements of the volunteer test subjects’ heads during frontal and lateral impacts by using active muscles. By representing intervertebral discs and spinal ligaments with solid parts and connecting them to streamlined vertebrae, Kleinberger [59] developed a full cervical spine model. However, there are some limitations in that the model did not account for muscle tissue, and the intervertebral disc was presumptively made of a single substance. The simplification of the discs seems to be a commonality as Holzapfel et al. [60] failed to consider the viscoelastic effect of the AF laminae model in their full spine model.
De Jager et al. [61] adapted and executed a head-neck model with the integrated multibody finite element code, which van der Horst [62] additionally advanced as a multi-body model. The first use of tissue models was made by Deng et al. [63] who used nonlinear, viscoelastic FE elements to represent tissue under dynamic conditions rather than calibrated or assumed attributes. Active muscles were also incorporated into the Hill muscle model offering realistic muscle force and direction during neck flexion. Each cervical spine muscle is represented in this model by both an active component and a passive one. This is ideal for simulating many neck impact scenarios as they typically involve active muscle behavior.
Conclusions
In this study, the material property models and cervical spine models were reviewed. Great progress has been recorded, even though less effort has been devoted to developing FE models of the cervical spine than developing FE models of the lumbar or thoracic spine. The papers discussed here can offer fundamental knowledge for the creation of general models; however, a trend is emerging toward the incorporation of detailed joint models into motion-driven musculoskeletal models to estimate stress/strain and contact pressure on joints in diverse processes.
Acknowledgments
This research was supported by the Boca Raton Regional Hospital Foundation (award # SP 19-579).
Notes
Conflict of Interest
No potential conflict of interest relevant to this article was reported.
Author Contributions
Data acquisition: ML; analysis of data: ML; drafting of the manuscript: ML; conception and design: ML; critical revision: ML, RP, UD, JD, TO, CT, FV; administrative support: CT, FV; and supervision: CT, FV.

